CYBERSPACE: Mar 11, 2012

Sunday, March 11, 2012

NEWTON'S LAW OF UNIVERSAL GRAVITATION

NEWTON'S LAW OF UNIVERSAL GRAVITATION
(Article = http://en.wikipedia.org/wiki/Newton%27s_law_of_universal_gravitation)

Newton's law of universal gravitation states that every massive particle in the universe attracts every other massive particle with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. (Separately it was shown that large spherically-symmetrical masses attract and are attracted as if all their mass were concentrated at their centers.) This is a general physical law derived from empirical observations by what Newton called induction.

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses.

where:

* F is the magnitude of the gravitational force between the two point masses,
* G is the gravitational constant,
* m1 is the mass of the first point mass,
* m2 is the mass of the second point mass, and
* r is the distance between the two point masses.

Assuming SI units, F is measured in newtons (N), m1 and m2 in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10−11 N m2 kg−2. The value of the constant G was first accurately determined from the results of the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798, although Cavendish did not himself calculate a numerical value for G. This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.

Vector form

Newton's law of universal gravitation can be written as a vector equation to account for the direction of the gravitational force as well as its magnitude. In this formula, quantities in bold represent vectors.

$\mathbf{F}_{12} = - G {m_1 m_2 \over {\vert \mathbf{r}_{12} \vert}^2} \, \mathbf{\hat{r}}_{12}$

where

F₁₂ is the force applied on object 2 due to object 1,

G is the gravitational constant,

m₁ and m₂ are respectively the masses of objects 1 and 2,

|r₁₂| = |r₂ − r₁| is the distance between objects 1 and 2, and

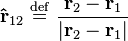$\mathbf{\hat{r}}_{12} \ \stackrel{\mathrm{def}}{=}\ \frac{\mathbf{r}_2 - \mathbf{r}_1}{\vert\mathbf{r}_2 - \mathbf{r}_1\vert}$ is the unit vector from object 1 to 2.

It can be seen that the vector form of the equation is the same as the scalar form given earlier, except that F is now a vector quantity, and the right hand side is multiplied by the appropriate unit vector. Also, it can be seen that F12 = −F21.

Gravitational field

The gravitational field is a vector field that describes the gravitational force which would be applied on an object in any given point in space, per unit mass. It is actually equal to the gravitational acceleration at that point.

http://upload.wikimedia.org/wikipedia/commons/thumb/b/b2/Gravityroom.svg/200px-Gravityroom.svg.png

http://upload.wikimedia.org/wikipedia/commons/thumb/5/5c/Gravitymacroscopic.svg/200px-Gravitymacroscopic.svg.png

It is a generalization of the vector form, which becomes particularly useful if more than 2 objects are involved (such as a rocket between the Earth and the Moon). For 2 objects (e.g. object 2 is a rocket, object 1 the Earth), we simply write r instead of r12 and m instead of m2 and define the gravitational field g(r) as:

$\mathbf g(\mathbf r) = - G {m_1 \over {{\vert \mathbf{r} \vert}^2}} \, \mathbf{\hat{r}}$

so that we can write:

$\mathbf{F}( \mathbf r) = m \mathbf g(\mathbf r)$

This formulation is dependent on the objects causing the field. The field has units of acceleration; in SI, this is m/s2.

Gravitational acceleration

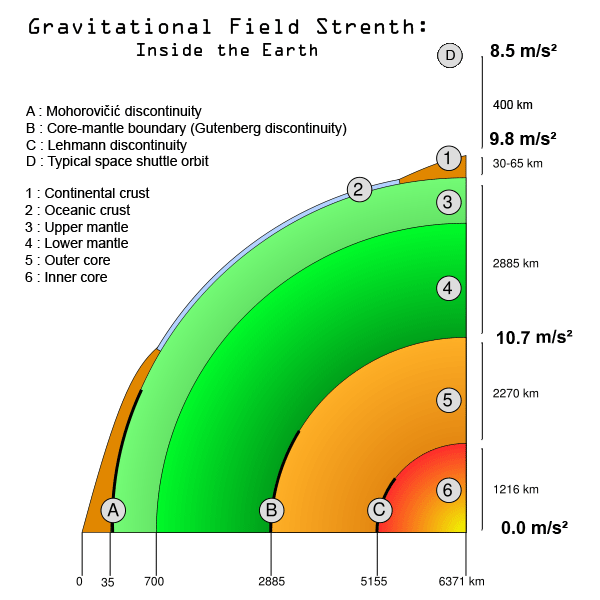
In physics, gravitational acceleration is the specific force or acceleration on an object caused by gravity. In a vacuum, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass. This is true regardless of the mass or composition of the body. On the surface of the Earth, all objects fall with an acceleration between 9.78 and 9.82 m/s2 depending on latitude, with a conventional standard value of exactly 9.80665 m/s2 (approx. 32.174 ft/s2). Objects with low densities do not accelerate as rapidly due to buoyancy and air resistance. In a vacuum all small objects have same acceleration regardless of density.

http://upload.wikimedia.org/wikipedia/commons/4/43/Earth-G-force.png

The barycentric gravitational acceleration at a point in space is given by:

$\mathbf{\hat{g}}=-{G M \over r^2}\mathbf{\hat{r}}$

where:

M is the mass of the attracting object,
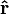$\mathbf{\hat{r}}$ is the unit vector from center of mass of the attracting object to the center of mass of the object being accelerated.
r is the distance between the two objects.
G is the gravitational constant of the universe.

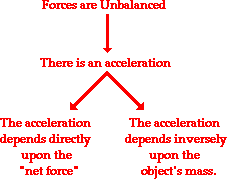
The relative acceleration of two the objects in the reference frame of the attracting object is:

$\mathbf{\hat{g}} = -{G( M+m ) \over r^2}\mathbf{\hat{r}}$

The relative acceleration depends on both masses.

Disregarding air resistance and the Earth's movement towards falling objects, all masses (large or small) dropped simultaneously will hit the ground at the same time. All masses lifted one at a time and dropped will hit the ground at the same time.

In General Relativity

In Einstein's theory of general relativity, gravitation is an attribute of curved spacetime instead of being due to a force propagated between bodies. In Einstein's theory, masses distort spacetime in their vicinity, and other particles move in trajectories determined by the geometry of spacetime. The gravitational force is a fictitious force; the gravitational acceleration of a body in free fall is due to its world line being a geodesic of spacetime.

NEWTON'S LAWS OF MOTION

NEWTON'S LAWS OF MOTION
(Article = http://www.physicsclassroom.com/class/newtlaws/)

Newton's First Law

Newton's first law of motion - sometimes referred to as the law of inertia.

An object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force.

Newton's Second Law

Newton's second law of motion pertains to the behavior of objects for which all existing forces are not balanced.

The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.

The second law states that the acceleration of an object is dependent upon two variables - the net force acting upon the object and the mass of the object. The acceleration of an object depends directly upon the net force acting upon the object, and inversely upon the mass of the object. As the force acting upon an object is increased, the acceleration of the object is increased. As the mass of an object is increased, the acceleration of the object is decreased.

This verbal statement can be expressed in equation form as follows:

a = F_net / m

The above equation is often rearranged to a more familiar form as shown below. The net force is equated to the product of the mass times the acceleration.

**F_net = m * a**

Newton's Third Law

For every action, there is an equal and opposite reaction.

The statement means that in every interaction, there is a pair of forces acting on the two interacting objects. The size of the forces on the first object equals the size of the force on the second object. The direction of the force on the first object is opposite to the direction of the force on the second object. Forces always come in pairs - equal and opposite action-reaction force pairs.

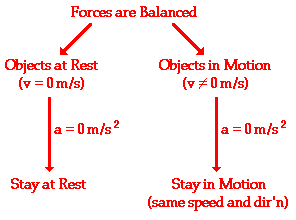
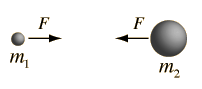
A variety of action-reaction force pairs are evident in nature. Consider the propulsion of a fish through the water. A fish uses its fins to push water backwards. But a push on the water will only serve to accelerate the water. Since forces result from mutual interactions, the water must also be pushing the fish forwards, propelling the fish through the water. The size of the force on the water equals the size of the force on the fish; the direction of the force on the water (backwards) is opposite the direction of the force on the fish (forwards). For every action, there is an equal (in size) and opposite (in direction) reaction force. Action-reaction force pairs make it possible for fish to swim.

Consider the flying motion of birds. A bird flies by use of its wings. The wings of a bird push air downwards. Since forces result from mutual interactions, the air must also be pushing the bird upwards. The size of the force on the air equals the size of the force on the bird; the direction of the force on the air (downwards) is opposite the direction of the force on the bird (upwards). For every action, there is an equal (in size) and opposite (in direction) reaction. Action-reaction force pairs make it possible for birds to fly.

PERIODIC TABLE OF ELEMENT

PERIODIC TABLE OF ELEMENT

(Article = http://en.wikipedia.org/wiki/Periodic_table)

http://www.homework-help-secrets.com/images/periodic-table-rev99.jpg

The periodic table of the chemical elements (also periodic table of the elements or just periodic table) is a tabular display of the chemical elements. Although precursors to this table exist, its invention is generally credited to Russian chemist Dmitri Mendeleev in 1869, who intended the table to illustrate recurring ("periodic") trends in the properties of the elements. The layout of the table has been refined and extended over time, as new elements have been discovered, and new theoretical models have been developed to explain chemical behavior.

The periodic table is now ubiquitous within the academic discipline of chemistry, providing a useful framework to classify, systematize, and compare all of the many different forms of chemical behavior. The table has found many applications in chemistry, physics, biology, and engineering, especially chemical engineering. The current standard table contains 118 elements as of March 2010 (elements 1–118).

Element categories in the periodic table

Metals						Metalloids	Nonmetals			Unknown chemical properties
Alkali metals	Alkaline earth metals	Inner transition elements		Transition elements	Other metals		Other nonmetals	Halogens	Noble gases
		Lanthanides	Actinides

**Atomic number colors show state at standard temperature and pressure (0 °C and 1 atm)**
Solids	Liquids	Gases	Unknown

**Borders show natural occurrence**
Primordial	From decay	Synthetic	(Undiscovered)

Complex Numbers & The Quadratic Formula

Complex Numbers & The Quadratic Formula

You'll probably only use complexes in the context of solving quadratics for their zeroes. (There are many other practical uses for complexes, but you'll have to wait for more interesting classes like "Engineering 201" to get to the "good stuff".)

Remember that the Quadratic Formula solves "ax2 + bx + c = 0" for the values of x. Also remember that this means that you are trying to find the x-intercepts of the graph. When the Formula gives you a negative inside the square root, you can now simplify the zero by using complex numbers. The answer you come up with is a valid "zero" or "root" or "solution" for "ax2 + bx + c = 0", because, if you plug it back into the quadratic, you'll get zero after you simplify. but you cannot graph a complex number on the x,y-plane. So this "solution to the equation" is not an x-intercept. In other words, you can make this connection between the Quadratic Formula, complex numbers, and graphing:

As an aside, you can graph complexes, but not in the x,y-plane. You need the "complex" plane. For the complex plane, the x-axis is where you plot the real part, and the y-axis is where you graph the imaginary part. For instance, for the complex number 3 – 2i, you would graph it like this:

This leads to an interesting fact: When you learned about regular ("real") numbers, you also learned about their order (this is what you show on the number line). But x,y-points don't come in any particular order. You can't say that one point "comes after" another point in the same way that you can say that one number comes after another number. For instance, you can't say that (4, 5) "comes after" (4, 3)" in the way that you can say that 5 comes after 3. Pretty much all you can do is compare "size", and, for complex numbers, "size" means "how far from the origin". To do this, you use the Distance Formula, and compare which complexes are closer to or further from the origin. This "size" concept is called "the modulus". For instance, looking at our complex number plotted above, its modulus is computed by using the Distance Formula:

Note that all points at this distance from the origin have the same modulus. All the points on the circle with radius sqrt(13) are viewed as being complex numbers having the same "size" as 3 – 2i.

Operations on Complex Numbers

Operations on Complex Numbers

Complex numbers are "binomials" of a sort, and are added, subtracted, and multiplied in a similar way. (Division, which is further down the page, is a bit different.)

For this last example, if you learned "FOIL", FOILing works for this kind of multiplication. But whatever method you use, remember that multiplying and adding with complexes works just like multiplying and adding polynomials, except that, while x2 is just x2, i2 is –1. That is, you can use the exact same techniques for simplifying complex-number expressions, but you can simplify even further with complexes than with polynomials, because i2 reduces to the number –1.

Adding and multiplying complexes isn't too bad. It's when you start on fractions (that is, division) that things turn ugly. Most of the reason for this ugliness is actually arbitrary. Remember back in elementary school, when you first learned fractions? Your teacher would get her panties in a wad if you used "improper" fractions. For instance, you couldn't say " 3/2 "; you had to convert it to "1 1/2". But now that you're in algebra, nobody cares, and you've probably noticed that "improper" fractions are often more useful than "mixed" fractions. The problem in the case of complexes is that your professor will get his boxers in a bunch if you leave imaginaries in the denominator. So how do you handle this?

Suppose you have the following problem:

The point here is that they want you to get rid of the i underneath. The 2 is fine, but the i has got to go. To do this, you use the fact that i2 = –1. If you multiply top and bottom by i, then the i underneath will vanish in a puff of negativity:

This was simple enough, but what if you have something more complicated?

Since you still have an i underneath, this didn't help much. So how do you handle this simplification? You use something called "conjugates". The conjugate of a complex number a + bi is the same number, but with the opposite sign in the middle: a – bi. When you multiply conjugates, you are, in effect, multiplying to a difference of squares:

Note that the i's disappeared. This is what the conjugate, difference-of-squares thing is for. Here's how it is used:

In the last step, note how the fraction was split into two pieces. This is because, technically speaking, a complex number is in two parts, the real part and the i part. They aren't supposed to "share" the denominator.

Complex Numbers: Introduction

Up until now, you've been told that you can't take the square root of a negative number. That's because you had no numbers that, when squared, were negative. Every number was positive after you squared it. So you couldn't very well square-root a negative and expect to come up with anything sensible.
Now, however, you can take the square root of a negative number, but it involves using a new number to do it. This new number was invented (discovered?) around the time of the Reformation. At this time, nobody believed that any "real world" use would be found for this new number, other than easing the computations involved in solving certain equations, so the new number was viewed as being a pretend number invented for convenience sake.
(But then, when you think about it, aren't all numbers inventions? It's not like numbers grow on trees! They live in our heads. We made them all up! Why not invent a new one, as long as it works okay with what we already have?)
Anyway, this new number is called "i", standing for "imaginary", because "everybody knew" that i wasn't "real". (That's why you couldn't take the square root of a negative number before: you only had "real" numbers; that is, numbers without the "i" in them.) The imaginary is defined to be:

But this doesn't make any sense! You already have two numbers that square to 1; namely –1 and +1. And i already squares to –1. So it's not reasonable that i would also square to 1. This points out an important detail: When dealing with imaginaries, you gain something (the ability to deal with negatives inside square roots), but you also lose something (some of the flexibility and convenient rules you used to have when dealing with square roots). In particular, YOU MUST ALWAYS DO THE i-PART FIRST!

In computations, you deal with i just as you would with x, except for the fact that x2 is just x2, but
i2 is –1:

Note this last problem. Within it, you can see that , because i2 = –1. Continuing, you get:

In other words, to calculate any high power of i, you can convert it to a lower power by taking the closest multiple of 4 that's no bigger than the exponent and subtracting this multiple from the exponent. For example, a common trick question on tests is something along the lines of "Simplify i99", the idea being that you'll try to multiply i ninety-nine times and you'll run out of time, and the teachers will get a good giggle at your expense in the faculty lounge. Here's how the shortcut works:

i99 = i96+3 = i(4×24)+3 = i3 = –i

That is, i99 = i3, because you can just lop off the i96. (Ninety-six is a multiple of four, so i96 is just 1, which you can ignore.) In other words, you can divide the exponent by 4 (using long division), discard the answer, and use only the remainder. This will give you the part of the exponent that you care above. Here are a few more examples:

Now you've seen how imaginaries work; it's time to move on to complex numbers. "Complex" numbers have two parts, a "real" part (being any "real" number that you're used to dealing with) and an "imaginary" part (being any number with an "i" in it). The "standard" format for complex numbers is "a + bi"; that is, real-part first and i-part last.

Capacitors and Inductors

Introduction

Two more linear, ideal basic passive circuit elements.
Energy storage elements stored in both magnetic and electric fields.
They found continual applications in more practical circuits such as filters, integrators, differentiators, circuit breakers and automobile ignition circuit.
Circuit analysis techniques and theorems applied to purely resistive circuits are equally applicable to circuits with inductors and capacitors.

Capacitors

Electrical component that consists of two conductors separated by an insulator or dielectric material.
Its behavior based on phenomenon associated with electric fields, which the source is voltage.
A time-varying electric fields produce a current flow in the space occupied by the fields.
Capacitance is the circuit parameter which relates the displacement current to the voltage.

Parallel capacitances

The equivalent capacitance of N parallel-connected capacitors is the sum of the individual capacitances.

Series capacitances

The equivalent capacitance of series-connected capacitors is the reciprocal of the sum of the reciprocals of the individual capacitances.

Inductors

Electrical component that opposes any change in electrical current.
Composed of a coil or wire wound around a non-magnetic core/magnetic core.
Its behavior based on phenomenon associated with magnetic fields, which the source is current.
A time-varying magnetic fields induce voltage in any conductor linked by the fields.
Inductance is the circuit parameter which relates the induced voltage to the current.

Series inductances

The equivalent inductance of N series-connected inductors is the sum of the individual inductances.

Parallel inductances

The equivalent inductance of series-connected inductors is the reciprocal of the sum of the reciprocals of the individual inductances.

Voltage Divider Rule (VDR) and Current Divider Rule (CDR)

Voltage Divider Rule (VDR)

Whenever voltage has to be divided among resistors in series use voltage divider rule principle.

Current Divider Rule (CDR)

Whenever current has to be divided among resistors in parallel, use current divider rule principle.

International System of Units (SI)

International System of Units (SI)

Multiplier	Prefix	Symbol
10¹⁸	Exa	E
10¹⁵	Peta	P
10¹²	Tera	T
10⁹	Giga	G
10⁶	Mega	M
10³	Kilo	k
10²	Hector	h
10¹	Deka	da
10^-1	Deci	d
10^-2	Centi	d
10^-3	Mili	m
10^-6	Micro	m
10^-9	Nano	n
10^-12	Pico	p
10^-15	Femto	f
10^-18	Atto	a

Series and Parallel Circuits

Series and Parallel Circuits

Series Equivalent Circuit

The equivalent resistance for any number of resistors in series connection is the sum of each individual resistor.

Apparently the single equivalent resistor is always larger than the largest resistor in the series connection.
Series resistors carry the same current thru them.
Voltage across each of the resistors obtained using voltage divider rule principle or Ohm’s law.

The equivalent resistance for any number of resistors in parallel connection is obtained by taking the reciprocal of the sum of the reciprocal of each single resistor in the circuit.

Apparently, the single equivalent resistor is always smaller than the smallest resistor in the parallel connection.
Voltage across each resistor must be the same.
Currents thru each of them are divided according to the current divider rule principle.

Page Select